(Voor Helen, in de hoop dat ze het gaat begrijpen en voor Lily, in de hoop dat ze het leuk gaat vinden.)

Door Jan Sepp

Dit stukje gaat over rekenen (en tekst opslaan) als een computer. Als je onder de veertig bent heb je dit op school gehad – en je bent het al lang weer vergeten. Dikke kans dat je het nooit gehad hebt als je boven de veertig bent. De praktische toepassing ervan is NUL, als je geen programmeur bent. Maar het is leuk om te weten wat er achter de schermen gebeurt.

Computers zijn doodsimpel: ze kunnen tot twee tellen en dan is het op. Dat begint nu (in 2020) heel voorzichtig te veranderen: het idee achter kwantumcomputers is in essentie dat ze tot vier kunnen tellen. Maar dat is toekomstmuziek, en ik moet nog zien dat die de komende tien jaar commercieel ingezet gaan worden.

Je computer denkt in hoge en lage voltages. Hij kan tot twee tellen, en dan zijn zijn mogelijkheden uitgeput. Nou, kennelijk niet, want anders zou hij niet heel nuttig zijn. Hoe werkt dat?

Decimaal

Kijk eerst maar even naar ons zelf. Wij zijn ooit begonnen op onze vingers te rekenen. Wij kunnen daarmee tot tien tellen, en dan is het op. En toch kunnen we grote getallen verwerken. Hoe doen we dat?

Wij hebben voor onze tien vingers tien kriebeltjes (of “tekens”, of “cijfers”¹of in het Engels “digit”, wat geestig is, want dat betekent ook vinger) bedacht. Waar letters per cultuur verschillen (bijna per land, denk maar aan de Nederlandse “IJ”) , zijn cijfers behoorlijk universeel. Ze zijn in de huidige vorm in de Middeleeuwen door de Arabieren bij ons geïntroduceerd.

Het begint met géén vinger: het cijfer nul, kriebeltje “0”. Dan één vinger: het cijfer één, kriebeltje “1”. Ik hoef het hopelijk niet verder uit te spellen, maar na het cijfer negen (“9”) zijn we door onze kriebeltjes heen. En dan? Daar heb je in Groep 2 of Groep 3 van de basisschool wekenlang op moeten oefenen: de overgang van “9” naar “10”. Daar gebeurt iets heel bijzonders: we hebben geen nieuw cijfer meer bedacht maar we werken met een combinatie van bestaande kriebeltjes! Niet alleen het cijfer zelf is van belang, maar ook de plaats van het cijfer. Om maar een willekeurig voorbeeld te noemen: “379” is iets heel anders dan “937” hoewel we dezelfde cijfers gebruiken. Dus: nul tot en met negen, dan een één ervoor en weer nul tot en met negen, dan een twee ervoor en weer nul tot en met negen, dan een drie ervoor … .

En wat als we door die twee posities heen zijn? Nu ligt de volgende stap voor de hand: 98, 99, 100, 101, 102 … 109, 110, 111 … 119, 120, 121 … 998, 999, 1000, 1001, 1002 … . Ik hoop van harte dat je dat niet moeilijk vindt. Niet moeilijk méér vindt want, nogmaals, op de Basisschool hebben ze flink wat inspanning verricht om je dit principe bij te brengen. En even voor alle zekerheid: 1000 is wat anders dan 10, juist omdat we de plaats ook belangrijk vinden. Op “99” volgt geen “10” maar “100”.

Nog eentje: “3790” is tien keer zo groot als “379” en “37900” is honderd keer zo groot. Kijk eens goed: iedere keer als je meer posities gebruikt vermenigvuldig je met tien:

7, 70, 700, 7000 … .

En zo heb je het ook geleerd. 3790, wat staat daar?

0 x 1
+ 9 x 10
+ 7 x 100
+3 x 1000

We werken van achter naar voren, van rechts naar links. De positie bepaalt wat een cijfer “waard” is en iedere keer als we een stapje meer naar links gaan vermenigvuldigen we de voorgaande positie met 10.

Tien cijfers dus, en dan beginnen we opnieuw. Niet alleen het cijfer zelf is van belang, maar ook de plaats van het cijfer. Dat is het decimale stelsel. De naam komt van het Latijnse “decem” dat “tien” betekent.

Andere talstelsels

En wat als we elf vingers hadden gehad? Of zeven? In het laatste geval hadden we ongetwijfeld maar zeven cijfers gehad. Dan zouden we als volgt geteld hebben: 0, 1, 2, 3, 4, 5, 6, 10, 11, 12, 13 … . Dus let op: 10 in het zeventallig stelsel is hetzelfde als 7 in het decimale stelsel. Noemt het geen 10, dat is verwarrend.

Overigens, echt lang geleden, zo’n 3.500 jaar, begonnen de eerste astronomen in Babylonië met het observeren van maan en zon. Zij ontdekten een cyclus waar het cijfer “6” veel in voorkwam. Zij bedachten het uur (10 keer 6 minuten), de dag (4 x 6 uur), de maand (5 keer 6 dagen) … Een zestallig stelsel. Ook daar heb je op school flink aan moeten wennen! Iemand heeft je, ooit, met veel liefde, bijgebracht dat het dertig minuten na 11:35 uur niet 11:65 uur is, maar vijf over twaalf!

Binair

Terug naar de computer. Die denkt niet in tien cijfers, niet in zeven of zes, maar in twee, namelijk hoge en lage voltages. (Of, als je dat liever hebt, “aan” of “uit”). Wij representeren dat als “1” of “0”: het binaire stelsel. De naam die we gebruiken voor de opslag van één zo’n binair cijfer is “bit” (een afkorting van binary digit). Dus de computer weet niet van het cijfer 2, of 3, of 9. Hij kent alleen de 0 en de 1, en dan is het op. En wat dan?

Dan doen we precies hetzelfde als in het decimale stelsel: als we door de cijfers heen zijn beginnen we opnieuw, met een “1” ervoor. Dat is ook betrekkelijk snel op. Kijk maar:

0, 1,
10, 11

en dan? Nou, net als wij doen bij 99, zetten we er weer een 1 voor en beginnen opnieuw:

0, 1,
10, 11,
100, 101, 110, 111,
1000, 1001, 1010, 1011, 1100, 1101, 1110 , 1111
10000 …

enzovoorts. Even voor alle zekerheid: Spreek binair “100” niet uit als honderd maar als vier. Zie je waarom? Kijk maar:

Die laatste is al best ingewikkeld. Je kunt het natellen in het rijtje hierboven, maar er is nog een truc. We weten dat binair “10” onze 2 is. Binair “100” is onze 4. Binair “1000” is onze 8. Nieuw: binair “10000” is onze 16. “100000” wordt 32. Kun je nu zelf afleiden wat “1000000” in onze decimale notatie is?

Juist, 64. Het is niet heel erg van belang, maar zie je ook dat die getallen steeds met 2 vermenigvuldigd worden? Nul en één zijn de uitzonderingen, maar zodra de positie van belang wordt gaat dat op: 2, 4, 8, 16, 32, 64, 128 … Als je erover nadenkt is dat heel logisch: iedere keer als je een positie meer gebruikt heb je twee keer zoveel mogelijkheden als bij het aantal posities ervoor.

We hebben hierboven 379 decimaal ontleed. We werken van rechts naar links:

(9 x 1) + (7 x 10) + (3 x 100) = 379

Dat kan ook binair. Maar nu vermenigvuldigen we niet met decimale tienen maar met binaire tweeën. Weer van rechts naar links. Dus binair 100101 is …

(1 x 1) + (0 x 2) + (1 x 4) + (0 x 8) + (0 x 16) + (1 x 32)
1 + 0 + 4 + 0 + 0 + 32 = 37

Binair 100101 is hetzelfde als decimaal 37. Overigens kan dat beduidend sneller met een “binary to decimal converter” op je rekenmachine (als je een wat duurdere hebt) of op het web:² Ik heb RapidTables.com gebruikt

Grote getallen

Grotere getallen worden al vrij snel ingewikkeld. Dat geldt zowel voor decimaal als binair. Wij moeten even twee keer kijken naar 35187605, en zetten er voor het gemak punten tussen (in Nederland, in Angelsaksische landen zijn het komma’s): 35.187.605. Ook dàt heb je moeten leren. Overigens vindt je (goedkope) rekenmachine het niet leuk als je er die punten tussen zet, die zijn er echt voor óns gemak.

Iets soortgelijks geldt voor grote binaire getallen: 1001001110100110. Wat staat daar in hemelsnaam? Ja, ik kan dat weer inkloppen in die binary to decimal converter, maar wat punten (of voor mijn part komma’s) ertussen zou toch wel prettig zijn. Op iedere derde positie een punt neerzetten heeft geen zin: we zouden veel, nog steeds onuitspreekbare, kleine binaire getallenreeksje krijgen.

Als je weet dat de vroegste computers acht bits tegelijk konden manipuleren dan ligt de grens voor de hand: we hebben “porties” gemaakt die de eerste computers behappen konden. Het Engels voor “portie” is “byte” en dat is precies waar het woord vandaan komt. (Grappig genoeg was het woord byte er voor het woord bit. Toen we bytes verder wilden onderverdelen zochten we een woord voor “een stukje van een byte”. Bit, dus.) En net zoals we decimale getallen verdelen in groepjes van drie cijfers, verdelen we grote binaire getallen in groepjes van 8 bits:

10010011 10100110

Maar pas op: dit is dus nog steeds één getal. Net zo min als een eenvoudige rekenmachine om kan gaan met onze punten kan hij dat met binaire bytes:

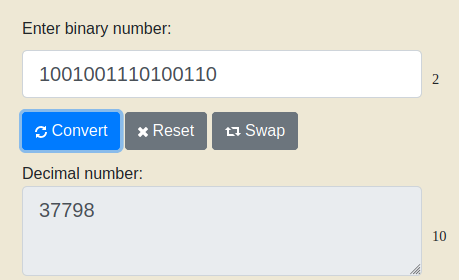
Als ik in plaats van 1001001110100110 zou invoeren 10010011 10100110 geeft deze converter een foutmelding. Bytes zijn er, als het om getallen gaat, voor óns gemak, niet voor dat van de computer.

Letters

De eerste computers waren in feite heel grote binaire rekenmachines en ze konden niet met letters of woorden omgaan. Maar toen het concept van de bytes eenmaal bedacht was, kwam er al gauw iemand op het idee: kunnen we zo’n groepje van 8 bits niet óók gebruiken om letters (en leestekens) weer te geven? Dus iets in de trant van: de letter A geven we weer als “01000001”, de letter B als “01000010”, de letter C als “01000011”, enzovoorts.

Dat kan, maar hoe onderscheiden we het getal “01000011” van de letter “01000011”? Dat is mensenwerk: de programmeur moet aangeven of hij hier een letter of een cijfer bedoelt. Als hij dat niet goed doet kan dat tot spectaculaire fouten leiden. Wat is de uitkomst van 381 + D? Juist, onzin. En je ziet het altijd weer gebeuren.

Niemand, echt niemand die het ooit doet, maar je kunt de tekst “Amsterdam” dus binair vertalen:

01000001 01101101 01110011 01110100 01100101 01110010 01100100 01100001 01101101

“Amsterdam” heeft negen letters, dus dat wordt weergegeven in 9 bytes. Nou ja, wij mensen doen dat nooit, maar de computer doet het met alles wat je intypt, en vertaalt het pas weer terug naar letters op het moment dat zo’n tekst op je beeldscherm of printer moet worden afgebeeld. Intern in de computer, en ook op je harde schijf, wordt alle tekst als 8-bits bytes opgeslagen.

Die letters zijn betrekkelijk willekeurig toegekend. De eersten die computers bouwden waren de Amerikanen en die hebben een code bedacht waarin ze alle Amerikaanse tekens (hoofdletters, kleine letters, cijfers (als kriebeltjes, niet als getal) en leestekens (spatie, komma, punt enzovoorts) kwijt kunnen. Dat is de ASCII tabel: American Standard Code for Information Interchange.

Het eerste bit gebruikten ze oorspronkelijk helemaal niet, dus we kunnen er twee tot de zevende (2⁷) 128 tekens in kwijt. Dat is ruim voldoende voor Amerikanen. Die oorspronkelijke ASCII tabel ziet er zo uit:

Die 7 bits waren dus oorspronkelijk voldoende voor de Amerikanen, Sterker nog: de hele linkerkolom (decimaal 0 t/m 31) bevat geen letters of leestekens, maar (opmaak-) aanwijzingen voor de computer. Als ergens in een tekst de code “0001001” [TAB] voorkomt, dan weet je tekstverwerker dat daar een tab ingevoerd moet worden. Iets soortgelijks geldt voor “000 0111” [BEL]: als die in een tekst voorkomt en je scrolt eroverheen krijg je een piepje (oorspronkelijk zo’n belletje als ook op typemachines zat).

UTF en codepages

Die 127 tekens waren dus voldoende voor de Amerikanen, maar niet voor de Fransen of de Denen, die er letters met accenten of rare “Ø”s bij willen hebben. Dat was nog makkelijk: in plaats van de ASCII tabel met 128 tekens gebruikten we er 256 – alle acht bits in een byte. Maar als je er niet-westerse tekens bij wil zetten (2 of drie verschillende Chinese tekensets, een stuk of wat Indiase, Japanse, Thaise, Arabische, Russische … ) dan kom je dik tekort. Dus gebruiken we tegenwoordig waar dat nodig is meer bytes om één letter weer te geven: de UTF code (Universal Transformation Format, ook wel Unicode genoemd).³Er is een fijn verschil tussen UTF en Unicode, maar dat is voor ons niet interessant. Lees het maar na op Wikipedia. Daarmee kun je 2³² verschillende tekens opslaan, meer dan een miljoen verschillende! Dat is genoeg om iedere cultuur ter wereld zijn eigen tekenset te geven.⁴Er is zelfs een Unicode representatie van middeleeuwse (westerse) letters!

Probleem opgelost? Nou … met UTF-32 gebruiken we voor een “A” nu geen acht bits meer (“0100 0001”) maar vier keer zoveel: 32 bits, dus vier bytes. Alles wat we met tekst doen kost ons dus vier keer zo veel ruimte! Anders gezegd, je harde schijf loopt vier keer zo snel vol. Om dat probleem op te lossen bestaan er verschillende UTF codes, waaronder UTF-8. En die lijkt sprekend op de ASCII-tabel!

Dan komt weer de vraag: hoe weet de computer met welke tekenset hij moet werken? 7-bits ASCII? 8-bits ASCII? UTF-8? UTF-16? UTF-32? Een eigen Microsoft tekenset? Wederom geldt: dat moet de programmeur vertellen. Als je een website aanmaakt, bijvoorbeeld, moet je in je HTML in de header opgeven welke “Codepage” je gaat gebruiken. Als je dat niet goed doet krijg je vreemde tekens. Waar in je uitvoer met de juiste codepage staat:

wordt dat met een andere codepage:

In Windows kun je als gebruiker ook je eigen codepages instellen. Mijn advies is: Blijf er vanaf!

Hexadecimaal

Hierboven schreef ik Amsterdam even in binaire tekens. Negen bytes nullen en enen, geen touw aan vast te knopen. Vandaar dat er een soort tussentaal ontwikkeld is waar je niet enorme hoeveelheden enen en nullen hoeft te interpreteren, maar waarin je toch dicht bij de binaire representatie blijft. We hadden daarvoor natuurlijk ons eigen, vertrouwde decimale stelsel kunnen gebruiken, maar dat heeft als nadeel dat je dat al heel gauw als getallen interpreteert. Erger nog: binair is niet goed om te zetten naar decimaal. We willen graag iets hebben waarin we zowel die nullen en enen als die letters naartoe kunnen vertalen. Sommigen prefereren het octale stelsel, waarin we acht verschillende kriebeltjes gebruiken, maar meestal wordt daarvoor het hexadecimale stelsel gebruikt. Hex is Latijn voor zes, dus het hexa-decimale stelsel kent 16 verschillende kriebeltjes. Alleen … wij kennen de 0 … 9, wat moeten we dan met die andere zes? We hadden hele nieuwe kriebeltjes kunnen bedenken, maar iemand heeft ervoor gekozen bestaande tekens te gebruiken, de letters “A” tot en met “F” (of “a” tot en met “f”, hoofd- en kleine letters mogen allebei). Voor alle zekerheid: dat zijn dus de (hexadecimale) cijfers A tot en met F! Dat ze er toevallig net zo uitzien als letters doet er niet toe. De “A” vervangt de decimale 10, de “B” de decimale elf, enzovoorts. Als volgt:

Zie je wat er gebeurt? We gaan veel later over op de “10”. Of, anders gezegd, hexadecimaal “10” is hetzelfde als decimaal “16”. Om decimale en hexadecimale getallen uit elkaar te houden geven we hexadecimaal een prefix: “0x”. Dus “10” en “0xA” betekenen hetzelfde, namelijk het cijfer dat volgt op “9”. (“9″in zowel decimaal als hexadecimaal. Mee eens?) Maar “0x10” vertalen we decimaal naar 16!

Hoe gaat het verder? Op een gegeven moment zitten we aan de 0x1F ( = 31) en dan wordt de volgende 0x20 (= 32). Eigenlijk precies hetzelfde als in het decimale stelsel: als we in hexadecimaal door onze (16) kriebeltjes heen zijn gaan we aan de voorkant over op het volgende kriebeltje. Decimaal 8, 9, 10, 11 … 18, 19, 20, 21 en hexadecimaal E, F, 10, 11 … 1E, 1F, 20, 21 … 2E, 2F, 30, 31 …
Pas op als je bij de 0x99 bent: 98, 99, 9A, 9B … 9E, 9F, A0, A1, A2 … AE, AF, B0, B1 …
en dan weer net zo lang tot je in de buurt van de 0xFF komt: FD, FE, FF, 100, 101 … enzovoort.

Dus op 0x99 volgt geen 0x100, maar 0x9A! Begrijp je in datzelfde rijtje die overgang van 0x9F naar 0xA0? In het decimale stelsel zijn we door onze kriebeltjes heen als we de negen gehad hebben. Maar in het hexadecimale stelsel hebben we dan nog 6 kriebeltjes te gaan. We gaan na de 0x9F gewoon door met het volgende kriebeltje na de negen (de A) en beginnen dan op de tweede positie weer bij 0 te tellen. Dus: op 0x9F volgt 0xA0!
Dat is niets anders dan in het decimale stelsel: je vindt het heel gewoon dat we na (decimaal) 49 overgaan naar een nieuw kriebeltje en daarachter weer bij 0 beginnen: juist, 50.
We zijn pas door onze hexadecimale kriebeltjes heen bij 0xFF. Als je dat doorhebt, dan heb je het begrepen.
Voor alle zekerheid: 0x100 is niet hetzelfde als decimaal 100, maar als decimaal 256!⁵Decimaal 100 is 10 keer 10, nietwaar? Hexadecimaal 100 is 0xF keer 0xF, oftewel (decimaal) 16 keer 16. Zelfde principe!

Hexadecimale dumps (hexdumps)

Je zou kunnen rekenen met hexadecimale getallen, en als je daar aan gewend bent is dat helemaal niet zo moeilijk. Iedere rekenmachine, ook de meest simpele, kan het. Maar wat is het grote voordeel als je toch al een rekenmachine tot je beschikking hebt? Dan kun je de berekening net zo goed meteen decimaal (of, voor de masochisten onder ons, binair) inkloppen. Nee, waar je dit echt goed voor kunt gebruiken is om die ASCII tabel wat gemakkelijker weer te geven. (Of de Unicode tabel, maar die wordt toch weer erg groot, gewoon omdat er heel veel tekens in zitten). Dat is de betekenis van die kolom Hex in de ASCII-tabel die ik eerder getoond heb. De letter “A” in de ASCII-tabel was binair “0100 0001” en in hexadecimaal 0x41. Dat laatste leest gemakkelijker.

Nog een keer het woord Amsterdam. Eerst nog een keer de bytes die we eerder tegenkwamen, en dan de hexadecimale representatie van die bytes:

In ieder geval neemt de hexadecimale representatie van de letters minder ruimte in. En als je het gewend bent, lees je hexadecimaal weergegeven tekens net zo gemakkelijk als ons alfabet – nogmaals: dat heb je ook met veel moeite geleerd! Met name programmeurs die willen kijken wat er werkelijk gebeurt kunnen een “hexdump” (hexadecimale dump) maken van hun programmacode zoals die in het geheugen van de computer staat. Stel dat ik een tekstbestand heb waarin staat …

Dan wordt dat als hexdump:

Linker kolom: het aantal tekens dat aan de eerste letter voorafgaat. Brede middelste kolom: de hexadecimale weergave van mijn tekst. Rechter kolom: de tekst in ASCII-tekens – voor zover het programma dat vertalen kan. Dus de tekst “Hallo” is, hexadecimaal weergegeven, “48 61 6c 6c 6f”. Pak de ASCII tabel hierboven er maar bij!

Zie je in de hexdump in de rechter kolom na het uitroepteken op de bovenste regel die punt staan? Dat is een placeholder voor een niet-toonbaar teken. In dit geval de regelovergang, hex “Oa”. Zoek hem op in de ASCII tabel en je ziet dat die staat voor het teken “[LF]” – linefeed. Dus, vertaald, regelovergang. Klopt precies! Dat is het grote voordeel van een hexdump: ook tekens die je normaal niet kunt zien worden afgebeeld.

Dit is super-interessant voor programmeurs. Als je wilt weten wat je programma werkelijk doet in het geheugen van de computer kun je een hexdump maken. Voor veel programmeurs is (of was, tegenwoordig zijn er meer sophisticated methoden) dat bijna dagelijkse kost. Ik heb professionele programmeurs gezien die hele grote hexdumps doorbladerden alsof het De Telegraaf was, en bij bladzij 7 uitriepen: “Ja, maar dìt kan niet kloppen!” En als je eenmaal weet waar de fout zit, kun je hem meestal vrij gemakkelijk oplossen.

Als gebruiker⁶Alleen programmeurs en de junkiebond noemen hun klanten “gebruikers” zul je heel weinig met hexadecimaal of hexdumps te maken hebben, maar nu weet je hoe het achter de schermen werkt.

Besluit

Ik ben begonnen bij decimaal, en ik heb benadrukt dat het je tenminste een schooljaar heeft gekost voor je decimale getallen een beetje begreep. Daarna ben ik overgestapt op binaire getallen. Wanhoop niet als je ze niet meteen begrijpt. Kom nog eens terug en lees dit stuk nog eens na (of zoek op Google naar “binary numbers”). Met binaire getallen kun je net zo goed rekenen als met decimale getallen, je bent het alleen niet gewend. De computer kan absoluut niet omgaan met decimaal, die moet per sé binaire getallen hebben.

Daarna heb ik een stap genomen en heb getoond dat je ook letters (en leestekens) binair kunt weergeven. In eerste instantie leken 7 bits genoeg, tegenwoordig gebruiken we er maximaal 32, waarmee je iedere letter (of ideogram, of hiëroglief) zijn eigen plaats in een tabel kunt geven. Die vertaaltabel van zeven bits is vastgelegd in de ASCII tabel. Voor niet-westerse “codepages” heb je één of andere vorm van UTF (ook wel Unicode genoemd) nodig.

Tenslotte heb ik “hexadecimaal” behandeld: een notatie tussen binair en ASCII in. Die wordt hoofdzakelijk door programmeurs gebruikt om de ASCII-tabel leesbaarder te maken.